2127：参加会议的最多员工数（2449 分）

力扣第 274 场周赛第 4 题

题目

一个公司准备组织一场会议，邀请名单上有 n 位员工。公司准备了一张 圆形 的桌子，可以坐下 任意数目 的员工。

员工编号为 0 到 n - 1 。每位员工都有一位 喜欢 的员工，每位员工 当且仅当 他被安排在喜欢员工的旁边，他才会参加会议。每位员工喜欢的员工 不会 是他自己。

给你一个下标从 0 开始的整数数组 favorite ，其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的 最多员工数目 。

示例 1：

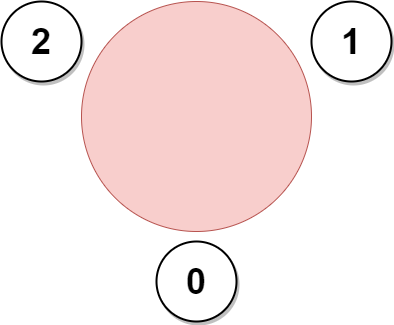
输入：favorite = [2,2,1,2]
输出：3
解释：
上图展示了公司邀请员工 0，1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议，因为员工 2 没办法同时坐在 0，1 和 3 员工的旁边。
注意，公司也可以邀请员工 1，2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。

示例 2：

输入：favorite = [1,2,0]
输出：3
解释：
每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。
座位安排同图 1 所示：
- 员工 0 坐在员工 2 和 1 之间。
- 员工 1 坐在员工 0 和 2 之间。
- 员工 2 坐在员工 1 和 0 之间。
参与会议的最多员工数目为 3 。

示例 3：

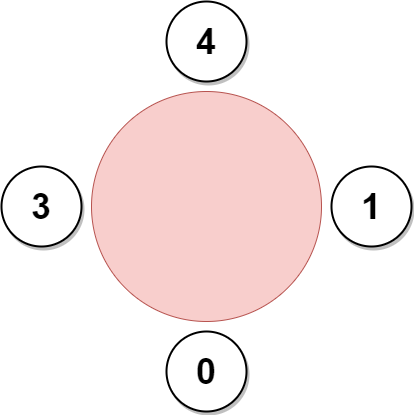
输入：favorite = [3,0,1,4,1]
输出：4
解释：
上图展示了公司可以邀请员工 0，1，3 和 4 参加会议以及他们在圆桌上的座位。
员工 2 无法参加，因为他喜欢的员工 1 旁边的座位已经被占领了。
所以公司只能不邀请员工 2 。
参加会议的最多员工数目为 4 。

提示：

• n == favorite.length
• 2 <= n <= 105
• 0 <= favorite[i] <= n - 1
• favorite[i] != i

分析

2360升级版，依然是内向基环树森林，注意有两种情况：

• 假如基环大于两个节点，只能坐一个基环，等价于问题 2360
• 假如基环只有两个节点，还可以坐这两个节点对应的最长链
  • 最长链长可以在拓扑排序时递推得出
  • 这样的基环可以同时坐多个
• 最后取两种情况的最大值即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution:
    def maximumInvitations(self, favorite: List[int]) -> int:
        F = favorite
        n = len(F)
        ind = [0]*n
        for f in F:
            ind[f] += 1
        Q = deque(u for u in range(n) if ind[u]==0)
        d = [0]*n
        while Q:
            u = Q.popleft()
            v = F[u]
            d[v] = max(d[v],d[u]+1)
            ind[v] -= 1
            if ind[v]==0:
                Q.append(v)
        res1,res2 = 0,0
        for u in range(n):
            if ind[u]:
                t = 0
                while ind[u]:
                    ind[u]=0
                    u = F[u]
                    t += 1
                if t==2:
                    res2 += t+d[u]+d[F[u]]
                else:
                    res1 = max(res1,t)
        return max(res1,res2)

208 ms