0684：冗余连接（★）

2016-11-14 约 602 字预计阅读 2 分钟次阅读

力扣第 684 题

题目

树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [a_i, b_i] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

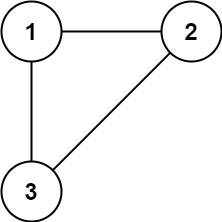
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

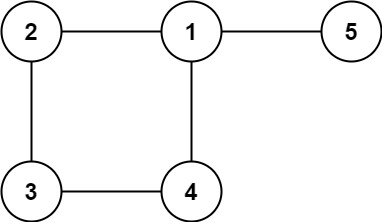
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

相似问题：

分析

#1

典型的并查集应用。遍历边，如果两个顶点已经连通则返回，否则就连通。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        def find(x):
            if f[x] != x:
                f[x] = find(f[x])
            return f[x]

        def union(x, y):
            f[find(x)] = find(y)

        f = list(range(len(edges) + 1))
        for u, v in edges:
            if find(u) == find(v):
                return [u, v]
            union(u, v)

37 ms

#2

也可以用拓扑排序：

先将所有入度为 1 的顶点入队
每轮弹出队首，将后继顶点的入度减 1，并将入度变为 1 的顶点入队
循环直到队空，剩下的环中的顶点的入度都大于 1
返回最后一条剩下的边即可

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)
        g = [[] for _ in range(n+1)]
        deg = [0]*(n+1)
        for a,b in edges:
            g[a].append(b)
            g[b].append(a)
            deg[a] += 1
            deg[b] += 1
        Q = deque(u for u in range(n+1) if deg[u]==1)
        while Q:
            u = Q.popleft()
            for v in g[u]:
                deg[v]-=1
                if deg[v]==1:
                    Q.append(v)
        for a,b in edges[::-1]:
            if deg[a]>1 and deg[b]>1:
                return [a,b]

33 ms

目录

0684：冗余连接（★）

题目

分析

#1

#2

解答