2360：图中的最长环（1897 分）

Ian

2022-07-31 约 580 字预计阅读 2 分钟次阅读

力扣第 304 场周赛第 4 题

题目

给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，其中每个节点至多有一条出边。

图用一个大小为 n 下标从 0 开始的数组 edges 表示，节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边，那么 edges[i] == -1 。

请你返回图中的最长环，如果没有任何环，请返回 -1 。

一个环指的是起点和终点是 同一个 节点的路径。

示例 1：

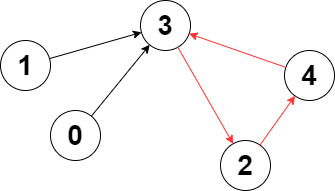
输入：edges = [3,3,4,2,3]
输出去：3
解释：图中的最长环是：2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ，所以返回 3 。

示例 2：

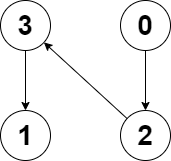
输入：edges = [2,-1,3,1]
输出：-1
解释：图中没有任何环。

提示：

n == edges.length
2 <= n <= 10⁵
-1 <= edges[i] < n
edges[i] != i

相似问题：

分析

#1

出度最多为1，是内向基环树森林，可以用拓扑排序去掉树枝，遍历剩下的环即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        n = len(edges)
        ind = [0]*n
        for u in edges:
            if u>=0:
                ind[u] += 1
        Q = deque(u for u in range(n) if ind[u]==0)
        while Q:
            u = Q.popleft()
            v =edges[u]
            if v>=0:
                ind[v] -= 1
                if ind[v]==0:
                    Q.append(v)
        res = -1
        for u in range(n):
            if ind[u]:
                w = 0
                while ind[u]:
                    ind[u]=0
                    u=edges[u]
                    w += 1
                res = max(res,w)
        return res

177 ms

#2

一种更简单的写法是从每个节点 u 出发，遍历直到遇到已访问节点 v
假如 v 在此次遍历的路径中，说明发现了一个新的环，可定位环长

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        n = len(edges)
        vis = [0]*n
        res = -1
        for u in range(n):
            A = []
            while u>=0 and not vis[u]:
                A.append(u)
                vis[u]=1
                u = edges[u]
            if u in A:
                res = max(res,len(A)-A.index(u))
        return res

147 ms

目录

2360：图中的最长环（1897 分）

题目

分析

#1

#2

解答