2876：有向图访问计数（2209 分）

力扣第 365 场周赛第 4 题

题目

现有一个有向图，其中包含 n 个节点，节点编号从 0 到 n - 1 。此外，该图还包含了 n 条有向边。

给你一个下标从 0 开始的数组 edges ，其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的边。

想象在图上发生以下过程：

• 你从节点 x 开始，通过边访问其他节点，直到你在 此过程 中再次访问到之前已经访问过的节点。

返回数组 answer 作为答案，其中 answer[i] 表示如果从节点 i 开始执行该过程，你可以访问到的不同节点数。

示例 1：

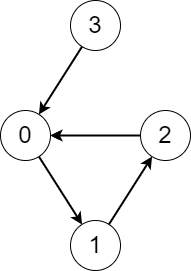
输入：edges = [1,2,0,0]
输出：[3,3,3,4]
解释：从每个节点开始执行该过程，记录如下：
- 从节点 0 开始，访问节点 0 -> 1 -> 2 -> 0 。访问的不同节点数是 3 。
- 从节点 1 开始，访问节点 1 -> 2 -> 0 -> 1 。访问的不同节点数是 3 。
- 从节点 2 开始，访问节点 2 -> 0 -> 1 -> 2 。访问的不同节点数是 3 。
- 从节点 3 开始，访问节点 3 -> 0 -> 1 -> 2 -> 0 。访问的不同节点数是 4 。

示例 2：

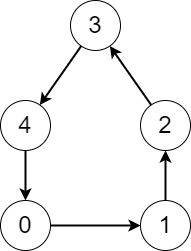
输入：edges = [1,2,3,4,0]
输出：[5,5,5,5,5]
解释：无论从哪个节点开始，在这个过程中，都可以访问到图中的每一个节点。

提示：

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] <= n - 1
• edges[i] != i

分析

2360 升级版，可以用拓扑排序，可以用更简单的依次遍历。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution:
    def countVisitedNodes(self, edges: List[int]) -> List[int]:
        n = len(edges)
        vis = [0]*n
        res = [0]*n
        for u in range(n):
            A = []
            while not vis[u]:
                A.append(u)
                vis[u] = 1
                u = edges[u]
            if u in A:
                i = A.index(u)
                for a in A[i:]:
                    res[a] = len(A)-i
                A = A[:i]
            for i,a in enumerate(A[::-1]):
                res[a] = res[u]+i+1
        return res

404 ms