1937:扣分后的最大得分(2105 分)
目录
题目
给你一个 m x n 的整数矩阵 points (下标从 0 开始)。一开始你的得分为 0 ,你想最大化从矩阵中得到的分数。
你的得分方式为:每一行 中选取一个格子,选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。
然而,相邻行之间被选中的格子如果隔得太远,你会失去一些得分。对于相邻行 r 和 r + 1 (其中 0 <= r < m - 1),选中坐标为 (r, c1) 和 (r + 1, c2) 的格子,你的总得分 减少 abs(c1 - c2) 。
请你返回你能得到的 最大 得分。
abs(x) 定义为:
- 如果
x >= 0,那么值为x。 - 如果
x < 0,那么值为-x。
示例 1:
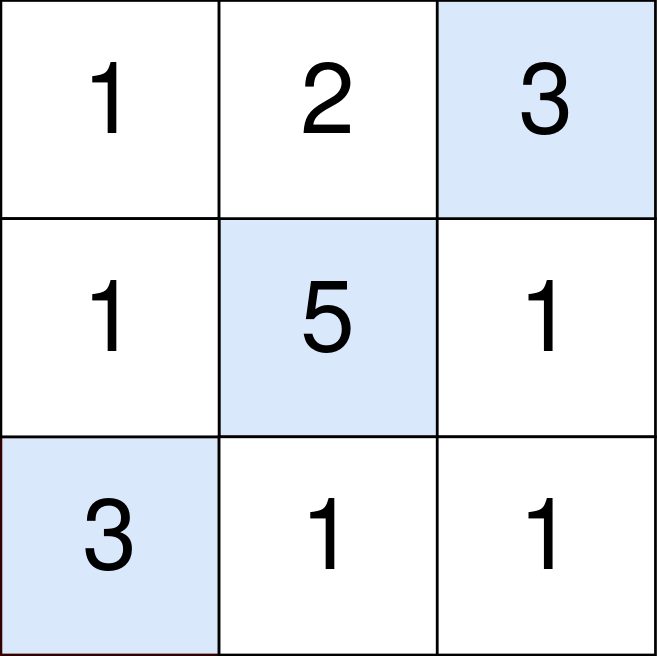
输入:points = [[1,2,3],[1,5,1],[3,1,1]] 输出:9 解释: 蓝色格子是最优方案选中的格子,坐标分别为 (0, 2),(1, 1) 和 (2, 0) 。 你的总得分增加 3 + 5 + 3 = 11 。 但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。 你的最终得分为 11 - 2 = 9 。
示例 2:
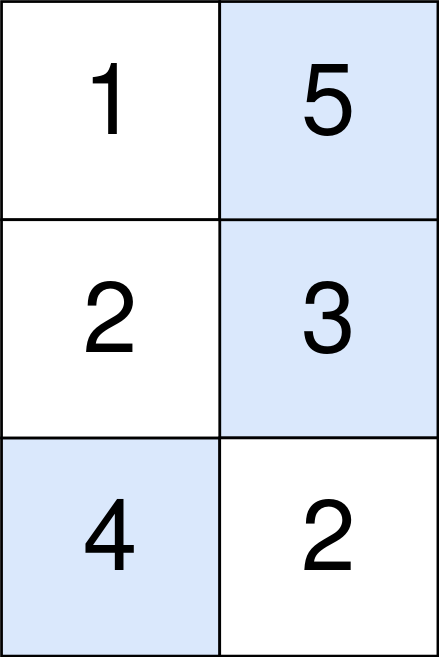
输入:points = [[1,5],[2,3],[4,2]] 输出:11 解释: 蓝色格子是最优方案选中的格子,坐标分别为 (0, 1),(1, 1) 和 (2, 0) 。 你的总得分增加 5 + 3 + 4 = 12 。 但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。 你的最终得分为 12 - 1 = 11 。
提示:
m == points.lengthn == points[r].length1 <= m, n <= 1051 <= m * n <= 1050 <= points[r][c] <= 105
相似问题:
分析
- 令 f[i][j] 代表前 i 行中,第 i 行选第 j 个格子的最大分,即得递推式
- f[i][j] = points[i][j]+max(f[i-1][k]-|k-j|)
- 拆掉绝对值,即是要求
- points[i][j]-j+max(f[i-1][k]+k),k<=j
- points[i][j]+j+max(f[i-1][k]-k),k>=j
- 显然可以预处理前/后缀最值,即可 O(1) 转移
解答
|
|
578 ms