0741：摘樱桃（★★）

Ian

2017-01-10 约 824 字预计阅读 2 分钟次阅读

力扣第 741 题

题目

给你一个 n x n 的网格 grid ，代表一块樱桃地，每个格子由以下三种数字的一种来表示：

0 表示这个格子是空的，所以你可以穿过它。
1 表示这个格子里装着一个樱桃，你可以摘到樱桃然后穿过它。
-1 表示这个格子里有荆棘，挡着你的路。

请你统计并返回：在遵守下列规则的情况下，能摘到的最多樱桃数：

从位置 (0, 0) 出发，最后到达 (n - 1, n - 1) ，只能向下或向右走，并且只能穿越有效的格子（即只可以穿过值为 0 或者 1 的格子）；
当到达 (n - 1, n - 1) 后，你要继续走，直到返回到 (0, 0) ，只能向上或向左走，并且只能穿越有效的格子；
当你经过一个格子且这个格子包含一个樱桃时，你将摘到樱桃并且这个格子会变成空的（值变为 0 ）；
如果在 (0, 0) 和 (n - 1, n - 1) 之间不存在一条可经过的路径，则无法摘到任何一个樱桃。

示例 1：

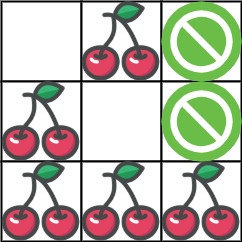
输入：grid = [[0,1,-1],[1,0,-1],[1,1,1]]
输出：5
解释：玩家从 (0, 0) 出发：向下、向下、向右、向右移动至 (2, 2) 。
在这一次行程中捡到 4 个樱桃，矩阵变成 [[0,1,-1],[0,0,-1],[0,0,0]] 。
然后，玩家向左、向上、向上、向左返回起点，再捡到 1 个樱桃。
总共捡到 5 个樱桃，这是最大可能值。

示例 2：

输入：grid = [[1,1,-1],[1,-1,1],[-1,1,1]]
输出：0

提示：

n == grid.length
n == grid[i].length
1 <= n <= 50
grid[i][j] 为 -1、0 或 1
grid[0][0] != -1
grid[n - 1][n - 1] != -1

相似问题：

分析

单程是个很显然的 dp 问题，双程则会互相影响，不能分开求。

那么考虑一起递推，到 (i,j) 位置的双程的最大值，依赖于上一步两条线路的结尾。

为了递推，令 dfs(i1,j1,i2,j2) 代表两条线路分别到 (i1,j1)、(i2,j2) 位置时的最大值，即可递推。

注意到递推过程中 i1+j1==i2+j2，因此可以简化为 dfs(k, i1, i2) 代表第 k 步两条线路分别到 (i1,k-i1)、(i2,k-i2) 位置时的最大值。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


class Solution:
def cherryPickup(self, grid: List[List[int]]) -> int:
    @lru_cache(None)
    def dfs(k, i1, i2):
        if k==0:
            return grid[0][0]
        if grid[i1][k-i1] == -1 or grid[i2][k-i2] == -1:
            return float('-inf')
        res, cur = float('-inf'), sum(grid[i][k-i] for i in {i1, i2})
        for x1, x2 in product([i1, i1-1], [i2, i2-1]):
            if min(x1, k-1-x1, x2, k-1-x2)>=0:
                res = max(res, cur+dfs(k-1, x1, x2))
        return res
    
    n = len(grid)
    return max(0, dfs(2*n-2, n-1, n-1))

1040 ms

目录

0741：摘樱桃（★★）

题目

分析

解答