0699：掉落的方块（★★）

2016-11-29 约 1113 字预计阅读 3 分钟次阅读

力扣第 699 题

题目

在二维平面上的 x 轴上，放置着一些方块。

给你一个二维整数数组 positions ，其中 positions[i] = [left_i, sideLength_i] 表示：第 i 个方块边长为 sideLength_i ，其左侧边与 x 轴上坐标点 left_i 对齐。

每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落，直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆，它就会固定在原地，无法移动。

在每个方块掉落后，你必须记录目前所有已经落稳的 方块堆叠的最高高度 。

返回一个整数数组 ans ，其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。

示例 1：

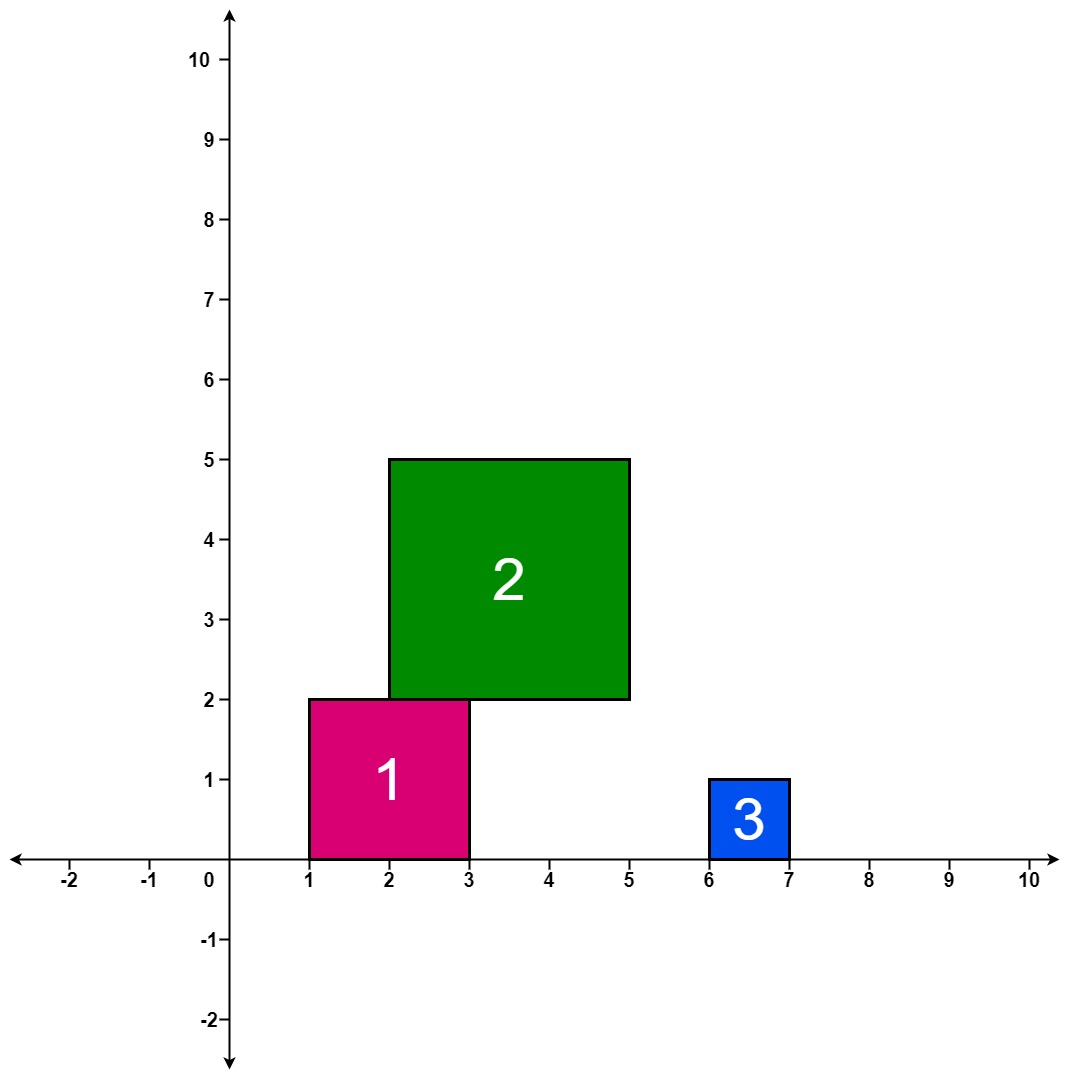
输入：positions = [[1,2],[2,3],[6,1]]
输出：[2,5,5]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 2 。
第 2 个方块掉落后，最高的堆叠由方块 1 和 2 组成，堆叠的最高高度为 5 。
第 3 个方块掉落后，最高的堆叠仍然由方块 1 和 2 组成，堆叠的最高高度为 5 。
因此，返回 [2, 5, 5] 作为答案。

示例 2：

输入：positions = [[100,100],[200,100]]
输出：[100,100]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 100 。
第 2 个方块掉落后，最高的堆叠可以由方块 1 组成也可以由方块 2 组成，堆叠的最高高度为 100 。
因此，返回 [100, 100] 作为答案。
注意，方块 2 擦过方块 1 的右侧边，但不会算作在方块 1 上着陆。

提示：

1 <= positions.length <= 1000
1 <= left_i <= 10⁸
1 <= sideLength_i <= 10⁶

相似问题：

0218：天际线问题

分析

#1

需要区间修改、区间查询，是线段树的典型应用
值域范围较大，需要动态开点
维护区间最大值即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


class Solution:
    def fallingSquares(self, positions: List[List[int]]) -> List[int]:
        def do(o,x):
            t[o] = max(t[o],x)
            f[o] = max(f[o],x)

        def down(o):
            if f[o]:
                do(o*2,f[o])
                do(o*2+1,f[o])
                f[o] = 0

        def update(a,b,x,o,l,r):
            if a<=l and r<=b:
                do(o,x)
                return 
            m = (l+r)//2
            down(o)
            if a<=m: update(a,b,x,o*2,l,m)
            if m<b: update(a,b,x,o*2+1,m+1,r)
            t[o] = max(t[o*2],t[o*2+1])
        
        def query(a,b,o,l,r):
            if a<=l and r<=b:
                return t[o]
            m = (l+r)//2
            down(o)
            res = 0
            if a<=m: res = query(a,b,o*2,l,m)
            if m<b: res = max(res,query(a,b,o*2+1,m+1,r))
            return res

        m = max(l+w-1 for l,w in positions)
        t = defaultdict(int)
        f = defaultdict(int)
        res = []
        for l,w in positions:
            r = l+w-1
            x = w+query(l,r,1,1,m)
            update(l,r,x,1,1,m)
            res.append(t[1])
        return res

854 ms

#2

由于每次区间查询完都会将整个区间重置为一个数，所以也可以用有序集合
令有序集合维护高度的轮廓线，即每一段的起点和高度
新加入方块 [l,r] 时
- 先二分找到覆盖的高度线段范围 [i,j]，i 为最后一个起点 <=l 的线段，j 为最后一个起点 <=r 的线段
- 遍历得到范围内的最大高度 h，l 处的高度应该变为 h+w
- r+1 处的高度有两种情况：
  - 若 r+1 是线段 j+1 的起点，保持不变
  - 否则，应该改为 j 线段的高度
- 起点在 [l,r] 范围内的线段都应该删除，特别注意：
  - [i+1,j] 的线段都应删除，i 线段则需要按起点判断是否删除
  - 删除和添加都会导致有序集合的下标变化，要注意处理，最好删除前先处理 r+1 处的高度，然后从后往前删，保证要处理的下标不变

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution:
    def fallingSquares(self, positions: List[List[int]]) -> List[int]:
        from sortedcontainers import SortedList
        sl = SortedList([(0,0)])
        res,ma = [],0
        for l,w in positions:
            r = l+w-1
            i = sl.bisect_left((l+1,))-1
            j = sl.bisect_left((r+1,))-1
            if j+1==len(sl) or sl[j+1][0]>r+1:
                sl.add((r+1,sl[j][1]))
            h = sl[i][1]
            for k in range(j,i,-1):
                h = max(h,sl.pop(k)[1])
            if sl[i][0]==l:
                sl.pop(i)
            sl.add((l,h+w))
            ma = max(ma,h+w)
            res.append(ma)
        return res

39 ms

目录

0699：掉落的方块（★★）

题目

分析

#1

#2

解答