3108:带权图里旅途的最小代价(2108 分)
题目
给你一个 n 个节点的带权无向图,节点编号为 0 到 n - 1 。
给你一个整数 n 和一个数组 edges ,其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间有一条权值为 wi 的无向边。
在图中,一趟旅途包含一系列节点和边。旅途开始和结束点都是图中的节点,且图中存在连接旅途中相邻节点的边。注意,一趟旅途可能访问同一条边或者同一个节点多次。
如果旅途开始于节点 u ,结束于节点 v ,我们定义这一趟旅途的 代价 是经过的边权按位与 AND 的结果。换句话说,如果经过的边对应的边权为 w0, w1, w2, ..., wk ,那么代价为w0 & w1 & w2 & ... & wk ,其中 & 表示按位与 AND 操作。
给你一个二维数组 query ,其中 query[i] = [si, ti] 。对于每一个查询,你需要找出从节点开始 si ,在节点 ti 处结束的旅途的最小代价。如果不存在这样的旅途,答案为 -1 。
返回数组 answer ,其中 answer[i] 表示对于查询 i 的 最小 旅途代价。
示例 1:
输入:n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]
输出:[1,-1]
解释:
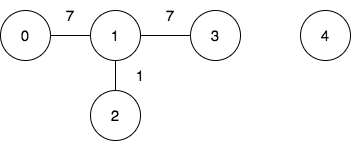
第一个查询想要得到代价为 1 的旅途,我们依次访问:0->1(边权为 7 )1->2 (边权为 1 )2->1(边权为 1 )1->3 (边权为 7 )。
第二个查询中,无法从节点 3 到节点 4 ,所以答案为 -1 。
示例 2:
输入:n = 3, edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]], query = [[1,2]]
输出:[0]
解释:
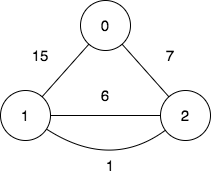
第一个查询想要得到代价为 0 的旅途,我们依次访问:1->2(边权为 1 ),2->1(边权 为 6 ),1->2(边权为 1 )。
提示:
1 <= n <= 1050 <= edges.length <= 105edges[i].length == 30 <= ui, vi <= n - 1ui != vi0 <= wi <= 1051 <= query.length <= 105query[i].length == 20 <= si, ti <= n - 1
分析
典型的并查集,求出每个连通块的最小代价即可。
解答
|
|
210 ms