2385：感染二叉树需要的总时间（1711 分）

Ian

2022-08-21 约 543 字预计阅读 2 分钟次阅读

力扣第 307 场周赛第 3 题

题目

给你一棵二叉树的根节点 root ，二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟，感染将会从值为 start 的节点开始爆发。

每分钟，如果节点满足以下全部条件，就会被感染：

节点此前还没有感染。
节点与一个已感染节点相邻。

返回感染整棵树需要的分钟数。

示例 1：

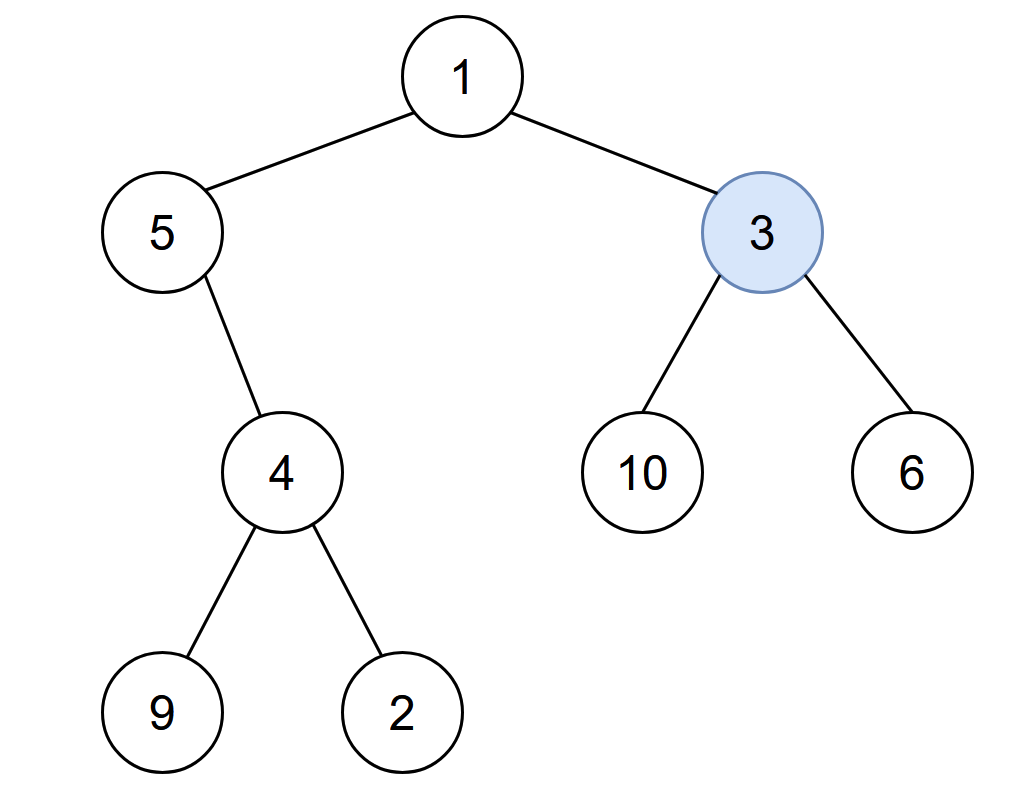
输入：root = [1,5,3,null,4,10,6,9,2], start = 3
输出：4
解释：节点按以下过程被感染：
- 第 0 分钟：节点 3
- 第 1 分钟：节点 1、10、6
- 第 2 分钟：节点5
- 第 3 分钟：节点 4
- 第 4 分钟：节点 9 和 2
感染整棵树需要 4 分钟，所以返回 4 。

示例 2：

输入：root = [1], start = 1
输出：0
解释：第 0 分钟，树中唯一一个节点处于感染状态，返回 0 。

提示：

树中节点的数目在范围 [1, 10⁵] 内
1 <= Node.val <= 10⁵
每个节点的值 互不相同
树中必定存在值为 start 的节点

分析

#1

最简单的是改成图的表达形式，bfs即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        g = defaultdict(list)
        sk = [root]
        while sk:
            u = sk.pop()
            for v in [u.left,u.right]:
                if v:
                    g[u.val].append(v.val)
                    g[v.val].append(u.val)
                    sk.append(v)
        Q = deque([(start,-1,0)])
        res = 0
        while Q:
            u,f,w = Q.popleft()
            for v in g[u]:
                if v!=f:
                    Q.append((v,u,w+1))
            res = w
        return res

364 ms

#2

也可以用树的递归解决：

令 dfs 返回 <子树高度，子树是否含有 start>
注意针对 start 节点，子树高度清零，即可递归

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        def dfs(u):
            if not u:
                return 0,0
            l1,l2 = dfs(u.left)
            r1,r2 = dfs(u.right)
            if u.val==start:
                self.res = max(self.res,l1,r1)
                return 1,1
            if l2 or r2:
                self.res = max(self.res,l1+r1)
                return l1+1 if l2 else r1+1,1
            return max(l1,r1)+1,0
        self.res = 0
        dfs(root)
        return self.res

261 ms

目录

2385：感染二叉树需要的总时间（1711 分）

题目

分析

#1

#2

解答