2003：每棵子树内缺失的最小基因值（2415 分）

力扣第 258 场周赛第 4 题

题目

有一棵根节点为 0 的 家族树 ，总共包含 n 个节点，节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ，其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ，所以 parents[0] == -1 。

总共有 105 个基因值，每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是节点 i 的基因值，且基因值 互不相同 。

请你返回一个数组 ans ，长度为 n ，其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小 基因值。

节点 x 为根的 子树 包含节点 x 和它所有的 后代 节点。

示例 1：

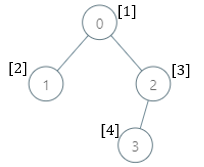
输入：parents = [-1,0,0,2], nums = [1,2,3,4]
输出：[5,1,1,1]
解释：每个子树答案计算结果如下：
- 0：子树包含节点 [0,1,2,3] ，基因值分别为 [1,2,3,4] 。5 是缺失的最小基因值。
- 1：子树只包含节点 1 ，基因值为 2 。1 是缺失的最小基因值。
- 2：子树包含节点 [2,3] ，基因值分别为 [3,4] 。1 是缺失的最小基因值。
- 3：子树只包含节点 3 ，基因值为 4 。1是缺失的最小基因值。

示例 2：

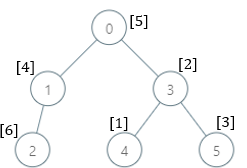
输入：parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
输出：[7,1,1,4,2,1]
解释：每个子树答案计算结果如下：
- 0：子树内包含节点 [0,1,2,3,4,5] ，基因值分别为 [5,4,6,2,1,3] 。7 是缺失的最小基因值。
- 1：子树内包含节点 [1,2] ，基因值分别为 [4,6] 。 1 是缺失的最小基因值。
- 2：子树内只包含节点 2 ，基因值为 6 。1 是缺失的最小基因值。
- 3：子树内包含节点 [3,4,5] ，基因值分别为 [2,1,3] 。4 是缺失的最小基因值。
- 4：子树内只包含节点 4 ，基因值为 1 。2 是缺失的最小基因值。
- 5：子树内只包含节点 5 ，基因值为 3 。1 是缺失的最小基因值。

示例 3：

输入：parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
输出：[1,1,1,1,1,1,1]
解释：所有子树都缺失基因值 1 。

提示：

• n == parents.length == nums.length
• 2 <= n <= 105
• 对于 i != 0 ，满足 0 <= parents[i] <= n - 1
• parents[0] == -1
• parents 表示一棵合法的树。
• 1 <= nums[i] <= 105
• nums[i] 互不相同。

分析

显然若基因值 1 不在树中，所有 ans 都为 1。 若基因值 1 在树中，对应的节点为 x，那么除了 x 和 x 的所有祖先，其它的 ans 都为 1。

然后可以递推 x 和 x 的祖先的 ans。 设 y 是 x 的父节点，那么从 ans[x] 遍历找到第一个不存在于 y 的子树的基因集合内的正整数即为 ans[y]。

在求 y 的子树的基因集合时，x 的子树无需再遍历。因此求基因集合的操作总共是 O(N) 时间。

递推 x 和 x 的祖先的 ans 时，ans 是递增的，因此遍历求 ans 的操作总共是 O(S) 时间（本题数据范围 S 等于节点个数范围 N)

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

def smallestMissingValueSubtree(self, parents: List[int], nums: List[int]) -> List[int]:
    n = len(nums)
    if 1 not in nums:
        return [1] * n
    nxt = defaultdict(list)
    for v, u in enumerate(parents):
        nxt[u].append(v)
    i = nums.index(1)
    ans, vis, cur = [1]*n, set(), 1
    while i != -1:
        queue = [i]
        while queue:
            vis |= {nums[u] for u in queue}
            queue = [v for u in queue for v in nxt[u] if nums[v] not in vis]
        while cur in vis:
            cur += 1
        ans[i] = cur
        i = parents[i]
    return ans

时间复杂度 O(N)，520 ms