力扣第 250 场周赛第 4 题
题目
给你一棵 n 个节点的有根树,节点编号从 0 到 n - 1 。每个节点的编号表示这个节点的 独一无二的基因值 (也就是说节点 x 的基因值为 x)。两个基因值的 基因差 是两者的 异或和 。给你整数数组 parents ,其中 parents[i] 是节点 i 的父节点。如果节点 x 是树的 根 ,那么 parents[x] == -1 。
给你查询数组 queries ,其中 queries[i] = [nodei, vali] 。对于查询 i ,请你找到 vali 和 pi 的 最大基因差 ,其中 pi 是节点 nodei 到根之间的任意节点(包含 nodei 和根节点)。更正式的,你想要最大化 vali XOR pi 。
请你返回数组 ans ,其中 ans[i] 是第 i 个查询的答案。
示例 1:
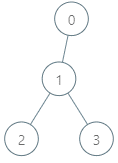
输入:parents = [-1,0,1,1], queries = [[0,2],[3,2],[2,5]]
输出:[2,3,7]
解释:查询数组处理如下:
- [0,2]:最大基因差的对应节点为 0 ,基因差为 2 XOR 0 = 2 。
- [3,2]:最大基因差的对应节点为 1 ,基因差为 2 XOR 1 = 3 。
- [2,5]:最大基因差的对应节点为 2 ,基因差为 5 XOR 2 = 7 。
示例 2:
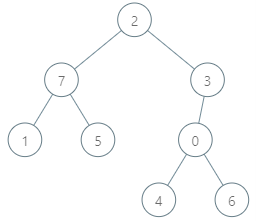
输入:parents = [3,7,-1,2,0,7,0,2], queries = [[4,6],[1,15],[0,5]]
输出:[6,14,7]
解释:查询数组处理如下:
- [4,6]:最大基因差的对应节点为 0 ,基因差为 6 XOR 0 = 6 。
- [1,15]:最大基因差的对应节点为 1 ,基因差为 15 XOR 1 = 14 。
- [0,5]:最大基因差的对应节点为 2 ,基因差为 5 XOR 2 = 7 。
提示:
2 <= parents.length <= 105- 对于每个 不是 根节点的
i ,有 0 <= parents[i] <= parents.length - 1 。
parents[root] == -11 <= queries.length <= 3 * 1040 <= nodei <= parents.length - 10 <= vali <= 2 * 105
相似问题:
分析
- 类似 1707,限制条件从值上界变为了树的路径
- 考虑遍历树并动态维护哈希表或字典树即可
- 注意动态维护过程中不仅有添加,还有删除,因此需要维护前缀的计数
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution:
def maxGeneticDifference(self, parents: List[int], queries: List[List[int]]) -> List[int]:
n = len(parents)
root = parents.index(-1)
g = [[] for _ in range(n)]
for u,v in enumerate(parents):
if v!=-1:
g[v].append(u)
L = max(n-1,max(x for _,x in queries)).bit_length()
d = defaultdict(list)
for i,(u,x) in enumerate(queries):
d[u].append((i,x))
T = [defaultdict(int) for _ in range(L)]
res = [0]*len(queries)
sk = [root]
while sk:
u = sk.pop()
if isinstance(u,str):
u = int(u)
for j in range(L):
T[j][u>>j] -= 1
continue
for j in range(L):
T[j][u>>j] += 1
for i,x in d[u]:
y = 0
for j in range(L-1,-1,-1):
y <<= 1
y += T[j][(y+1)^(x>>j)]>0
res[i] = y
sk.append(str(u))
sk.extend(g[u])
return res
|
2392 ms
*附加
字典树写法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
class BitTrie:
def __init__(self,n,L): # 插入总长度 n-1、最长 L 的二进制串
self.t = [[0]*n for _ in range(2)] # 模拟树节点
self.i = 0
self.L = L
self.s = [0]*n
def add(self, x):
p = 0
for j in range(self.L-1, -1, -1):
bit = (x>>j)&1
if not self.t[bit][p]:
self.i += 1
self.t[bit][p] = self.i
p = self.t[bit][p]
self.s[p] += 1
def remove(self,x):
p = 0
for j in range(self.L-1,-1,-1):
bit = (x>>j)&1
p = self.t[bit][p]
self.s[p]-=1
def maxxor(self,x):
p = 0
res = 0
for j in range(self.L-1, -1, -1):
bit = (x>>j)&1
q = self.t[bit^1][p]
if q and self.s[q]:
res |= 1 << j
bit ^= 1
p = self.t[bit][p]
return res
class Solution:
def maxGeneticDifference(self, parents: List[int], queries: List[List[int]]) -> List[int]:
n = len(parents)
root = parents.index(-1)
g = [[] for _ in range(n)]
for u,v in enumerate(parents):
if v!=-1:
g[v].append(u)
L = max(n-1,max(x for _,x in queries)).bit_length()
trie = BitTrie(n*L+1,L)
d = defaultdict(list)
for i,(u,x) in enumerate(queries):
d[u].append((i,x))
res = [0]*len(queries)
sk = [root]
while sk:
u = sk.pop()
if isinstance(u,str):
trie.remove(int(u))
continue
trie.add(u)
for i,x in d[u]:
res[i] = trie.maxxor(x)
sk.append(str(u))
sk.extend(g[u])
return res
|
2744 ms

