1857：有向图中最大颜色值（2312 分）

力扣第 240 场周赛第 4 题

题目

给你一个 有向图 ，它含有 n 个节点和 m 条边。节点编号从 0 到 n - 1 。

给你一个字符串 colors ，其中 colors[i] 是小写英文字母，表示图中第 i 个节点的 颜色 （下标从 0 开始）。同时给你一个二维数组 edges ，其中 edges[j] = [aj, bj] 表示从节点 aj 到节点 bj 有一条 有向边 。

图中一条有效 路径 是一个点序列 x1 -> x2 -> x3 -> ... -> xk ，对于所有 1 <= i < k ，从 xi 到 xi+1 在图中有一条有向边。路径的 颜色值 是路径中 出现次数最多 颜色的节点数目。

请你返回给定图中有效路径里面的 最大颜色值 。如果图中含有环，请返回 -1 。

示例 1：

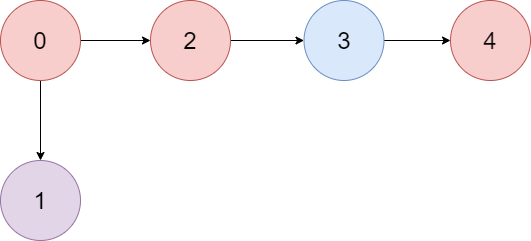
输入：colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
输出：3
解释：路径 0 -> 2 -> 3 -> 4 含有 3 个颜色为 "a" 的节点（上图中的红色节点）。

示例 2：

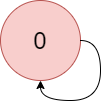
输入：colors = "a", edges = [[0,0]]
输出：-1
解释：从 0 到 0 有一个环。

提示：

• n == colors.length
• m == edges.length
• 1 <= n <= 105
• 0 <= m <= 105
• colors 只含有小写英文字母。
• 0 <= aj, bj < n

分析

要判断环，容易想到用拓扑排序。

若没有环，那么对于有向无环图，可以考虑用递归：

• 问题中要求路径中的最大颜色值，不好直接递归。容易递归的是每种颜色的最大值。
• 假设路径中的最大颜色值是 cnt，对应的颜色为 x，那么显然颜色 x 的最大值就是 cnt，其它颜色的最大值 <= cnt。
• 因此 max(每种颜色的最大值) 即为所求。

注意到拓扑排序出队的顺序和递推的顺序其实是一致的，因此可以同时进行。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:
    n = len(colors)
    nxt, indeg = defaultdict(list), [0]*n
    for u, v in edges:
        nxt[u].append(v)
        indeg[v] += 1
    res, dp = 0, [defaultdict(int) for _ in range(n)]
    queue = deque(u for u in range(n) if indeg[u]==0)
    while queue:
        u = queue.popleft()
        dp[u][colors[u]] += 1
        res = max(res, dp[u][colors[u]])
        for v in nxt[u]:
            indeg[v] -= 1
            if indeg[v] == 0:
                queue.append(v)
            for c in dp[u]:
                dp[v][c] = max(dp[v][c], dp[u][c])
    return res if all(indeg[u]==0 for u in range(n)) else -1

1812 ms