1819：序列中不同最大公约数的数目（2539 分）

力扣第 235 场周赛第 4 题

题目

给你一个由正整数组成的数组 nums 。

数字序列的 最大公约数 定义为序列中所有整数的共有约数中的最大整数。

• 例如，序列 [4,6,16] 的最大公约数是 2 。

数组的一个 子序列 本质是一个序列，可以通过删除数组中的某些元素（或者不删除）得到。

• 例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。

计算并返回 nums 的所有 非空 子序列中 不同 最大公约数的 数目 。

示例 1：

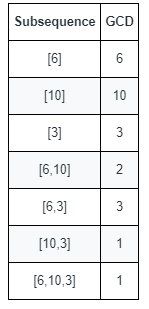
输入：nums = [6,10,3]
输出：5
解释：上图显示了所有的非空子序列与各自的最大公约数。
不同的最大公约数为 6 、10 、3 、2 和 1 。

示例 2：

输入：nums = [5,15,40,5,6]
输出：7

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 2 * 105

相似问题：

• 1979：找出数组的最大公约数（1184 分）

分析

要递推所有子序列的最大公约数时间复杂度高。注意到最大公约数不会超过 2*10^5， 因此可以反过来，判断每个数是否是某个子序列的最大公约数。

这样总时间不超过 N * 调和级数，时间复杂度 O(N*logN)。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def countDifferentSubsequenceGCDs(self, nums: List[int]) -> int:
    res, nums, Max = 0, set(nums), max(nums)
    for x in range(1, Max+1):
        g = None
        for y in range(x, Max+1, x):
            if y in nums:
                g = gcd(g, y) if g else y
                if g == x:
                    res += 1
                    break
    return res

2656 ms