1557：可以到达所有点的最少点数目（1512 分）

力扣第 33 场双周赛第 2 题

题目

给你一个 有向无环图 ， n 个节点编号为 0 到 n-1 ，以及一个边数组 edges ，其中 edges[i] = [fromi, toi] 表示一条从点 fromi 到点 toi 的有向边。

找到最小的点集使得从这些点出发能到达图中所有点。题目保证解存在且唯一。

你可以以任意顺序返回这些节点编号。

示例 1：

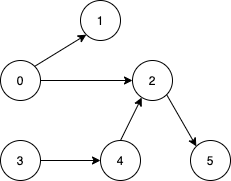
输入：n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
输出：[0,3]
解释：从单个节点出发无法到达所有节点。从 0 出发我们可以到达 [0,1,2,5] 。从 3 出发我们可以到达 [3,4,2,5] 。所以我们输出 [0,3] 。

示例 2：

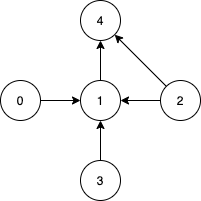
输入：n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
输出：[0,2,3]
解释：注意到节点 0，3 和 2 无法从其他节点到达，所以我们必须将它们包含在结果点集中，这些点都能到达节点 1 和 4 。

提示：

• 2 <= n <= 10^5
• 1 <= edges.length <= min(10^5, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi < n
• 所有点对 (fromi, toi) 互不相同。

分析

显然入度为 0 的节点无法由其他节点到达，所以必须在结果点集中。入度不为 0 的节点可以由其它节点到达，因此不需要添加。 所以返回所有入度为 0 的节点即可。

解答

1
2
3

def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:
	Set = set(b for _, b in edges)
	return [i for i in range(n) if i not in Set]

124 ms