1368：使网格图至少有一条有效路径的最小代价（2068 分）

力扣第 178 场周赛第 4 题

题目

给你一个 m x n 的网格图 grid 。 grid 中每个格子都有一个数字，对应着从该格子出发下一步走的方向。 grid[i][j] 中的数字可能为以下几种情况：

• 1 ，下一步往右走，也就是你会从 grid[i][j] 走到 grid[i][j + 1]
• 2 ，下一步往左走，也就是你会从 grid[i][j] 走到 grid[i][j - 1]
• 3 ，下一步往下走，也就是你会从 grid[i][j] 走到 grid[i + 1][j]
• 4 ，下一步往上走，也就是你会从 grid[i][j] 走到 grid[i - 1][j]

注意网格图中可能会有 无效数字 ，因为它们可能指向 grid 以外的区域。

一开始，你会从最左上角的格子 (0,0) 出发。我们定义一条 有效路径 为从格子 (0,0) 出发，每一步都顺着数字对应方向走，最终在最右下角的格子 (m - 1, n - 1) 结束的路径。有效路径 不需要是最短路径 。

你可以花费 cost = 1 的代价修改一个格子中的数字，但每个格子中的数字 只能修改一次 。

请你返回让网格图至少有一条有效路径的最小代价。

示例 1：

输入：grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
输出：3
解释：你将从点 (0, 0) 出发。
到达 (3, 3) 的路径为： (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) 花费代价 cost = 1 使方向向下 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) 花费代价 cost = 1 使方向向下 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) 花费代价 cost = 1 使方向向下 --> (3, 3)
总花费为 cost = 3.

示例 2：

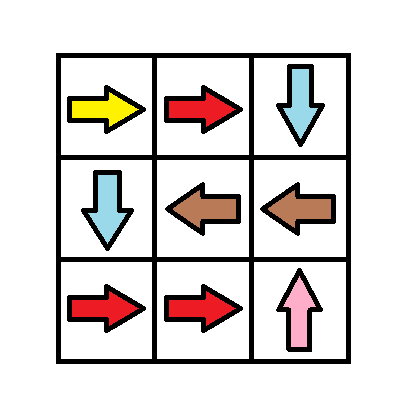
输入：grid = [[1,1,3],[3,2,2],[1,1,4]]
输出：0
解释：不修改任何数字你就可以从 (0, 0) 到达 (2, 2) 。

示例 3：

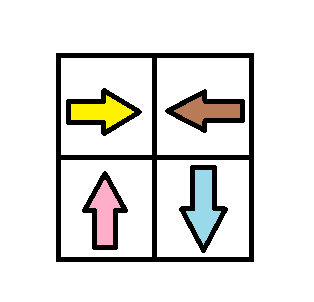
输入：grid = [[1,2],[4,3]]
输出：1

示例 4：

输入：grid = [[2,2,2],[2,2,2]]
输出：3

示例 5：

输入：grid = [[4]]
输出：0

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100

相似问题：

• 2203：得到要求路径的最小带权子图（2364 分）
• 2556：二进制矩阵中翻转最多一次使路径不连通（2368 分）

分析

将每个格子看作顶点，相邻格子的路径看作边，如果边的方向顺着数字，看作权重 0，否则权重 1。

那么就是典型的最短路问题，用 dijkstra 或者 01bfs 即可。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

def minCost(self, grid: List[List[int]]) -> int:
	m, n = len(grid), len(grid[0])
	Q, d = deque([(0, 0, 0)]), {}
	while Q:
		i, j, w = Q.popleft()
		if (i,j)==(m-1,n-1):
			return w
		if (i, j) in d:
			continue
		d[(i,j)] = w
		for x, y, k in [(i, j+1, 1), (i, j-1, 2), (i+1, j, 3), (i-1, j, 4)]:
			if 0<=x<m and 0<=y<n and (x, y) not in d:
				if grid[i][j]==k:
					Q.appendleft((x,y,w))
				else:
					Q.append((x,y,w+1))

180 ms