1104：二叉树寻路（1544 分）

力扣第 143 场周赛第 2 题

题目

在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

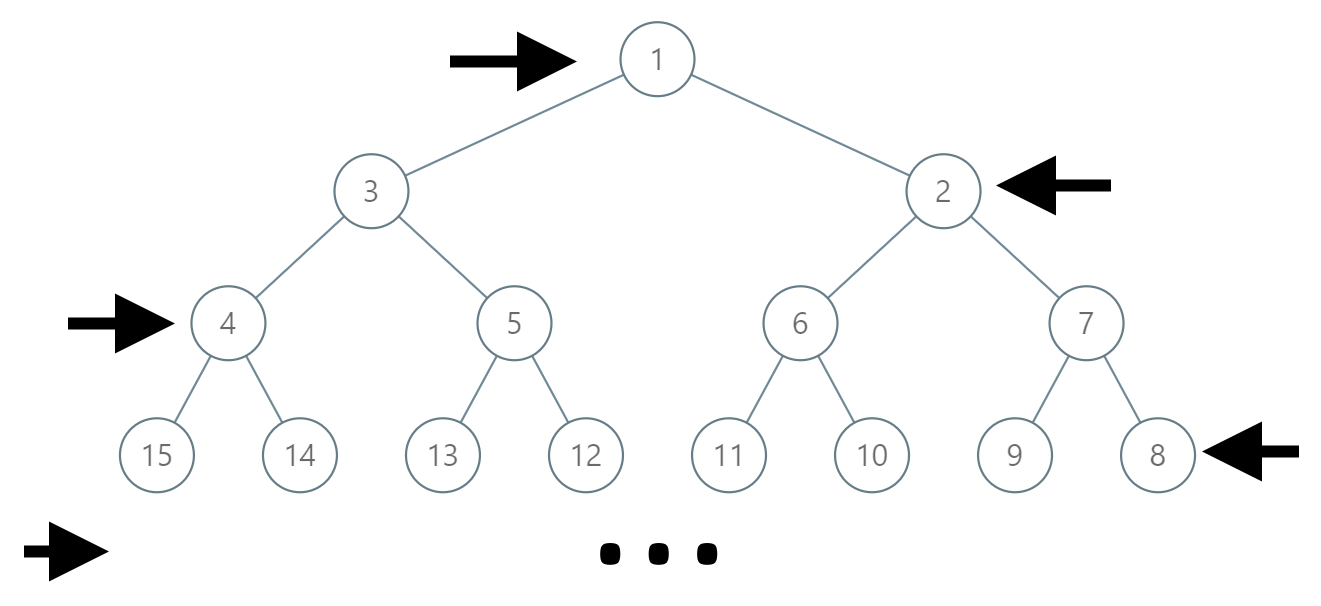
给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

示例 1：

输入：label = 14
输出：[1,3,4,14]

示例 2：

输入：label = 26
输出：[1,2,6,10,26]

提示：

• 1 <= label <= 10^6

分析

如果是原本的满二叉树，节点 x 的父节点就是 x//2，递推即可。 本题在偶数行反转了序号，因此需要找到 x 在该层对应的镜像节点 y，才是原本的序号。

第 h 层的序号范围是 [2^(h-1), 2^h-1]，因此 y = 2^(h-1)+2^h-1-x。 每层递推即可。

解答

1
2
3
4
5
6

def pathInZigZagTree(self, label: int) -> List[int]:
    res = [label]
    while label > 1:
        label = ((1 << (label.bit_length() - 1)) * 3 - 1 - label) // 2
        res.append(label)
    return res[::-1]

24 ms