0835：图像重叠（1969 分）

Ian

2018-05-13 约 566 字预计阅读 2 分钟次阅读

力扣第 84 场周赛第 3 题

题目

给你两个图像 img1 和 img2 ，两个图像的大小都是 n x n ，用大小相同的二进制正方形矩阵表示。二进制矩阵仅由若干 0 和若干 1 组成。

转换其中一个图像，将所有的 1 向左，右，上，或下滑动任何数量的单位；然后把它放在另一个图像的上面。该转换的重叠是指两个图像都具有 1 的位置的数目。

请注意，转换 不包括 向任何方向旋转。越过矩阵边界的 1 都将被清除。

最大可能的重叠数量是多少？

示例 1：

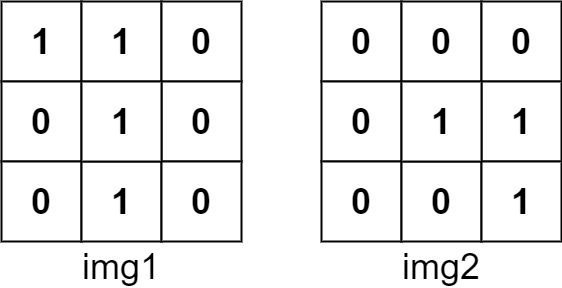
输入：img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]]
输出：3
解释：将 img1 向右移动 1 个单位，再向下移动 1 个单位。

两个图像都具有 1 的位置的数目是 3（用红色标识）。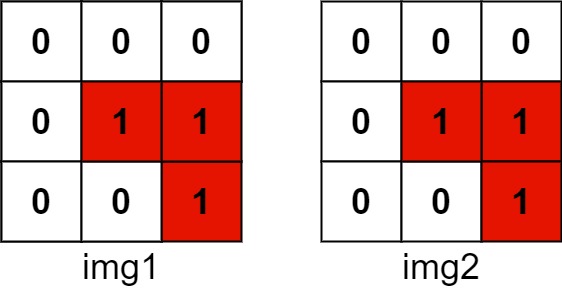

示例 2：

输入：img1 = [[1]], img2 = [[1]]
输出：1

示例 3：

输入：img1 = [[0]], img2 = [[0]]
输出：0

提示：

n == img1.length == img1[i].length
n == img2.length == img2[i].length
1 <= n <= 30
img1[i][j] 为 0 或 1
img2[i][j] 为 0 或 1

分析

数据范围较小，考虑暴力遍历。

令 x 代表 img1 水平滑动的单位，y 代表 img1 竖直滑动的单位，范围都是 [-(n-1), n-1]。遍历 <x, y>，求重叠的 1 的数目即可。

解答

1
2
3
4
5
6
7


def largestOverlap(self, img1: List[List[int]], img2: List[List[int]]) -> int:
    def cal(x, y):
        return sum(0<=i+x<n and 0<=j+y<n and img2[i+x][j+y]==1 for i, j in points)

    n = len(img1)
    points = [(i, j) for i in range(n) for j in range(n) if img1[i][j]]
    return max(cal(x, y) for x in range(-n+1, n) for y in range(-n+1, n))

时间复杂度 O(N^4)，892 ms

*附加

还可以用另一种方式计算重叠的 1 的数目：将重叠部分对应的两个数相乘，并全部求和。

这其实就类似于卷积，因此调用 scipy.signal.correlate2d 即可求出每种滑动方式对应的重叠的 1 的数目。

1
2
3


def largestOverlap(self, img1: List[List[int]], img2: List[List[int]]) -> int:
    from scipy.signal import correlate2d
    return int(correlate2d(img1, img2).max())

284 ms

目录

0835：图像重叠（1969 分）

题目

分析

解答

*附加