0834：树中距离之和（2197 分）

力扣第 84 场周赛第 4 题

题目

给定一个无向、连通的树。树中有 n 个标记为 0...n-1 的节点以及 n-1 条边 。

给定整数 n 和数组 edges ， edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。

返回长度为 n 的数组 answer ，其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。

示例 1:

输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。

示例 2:

输入: n = 1, edges = []
输出: [0]

示例 3:

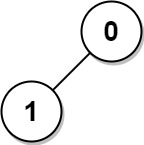
输入: n = 2, edges = [[1,0]]
输出: [1,1]

提示:

• 1 <= n <= 3 * 104
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 给定的输入保证为有效的树

相似问题：

• 0979：在二叉树中分配硬币（1709 分）
• 2049：统计最高分的节点数目（1911 分）
• 2603：收集树中金币（2711 分）
• 2925：在树上执行操作以后得到的最大分数（1939 分）
• 3067：在带权树网络中统计可连接服务器对数目（1908 分）

分析

• 典型的换根 dp，通用的方法是先 dfs 一次求出根节点 0 的值，然后再 dfs 一次，根据相邻节点的关系更新其它节点的值
• 本题中，第一次 dfs 时，求节点 u 到所有子节点的距离之和 f[u]
  • 除了知道每个子结点 v 的值 f[v] 外，还需要知道 v 的节点个数
  • 因此维护 sz[u] 表示 u 的节点个数，即可递推
  • dfs 结束后，f[0] 即是节点 0 的最终值
• 第二次 dfs 时，假如已知节点 u 的最终值为 g[u]
  • 对于 u 的子节点 v，v 相比于 u，到 v 的子节点的距离都少了 1，到其它节点的距离都多了 1
  • 因此可以递推 g[v]=g[u]-sz[v]+n-sz[v]

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution:
    def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:
        g = [[] for _ in range(n)]
        for a,b in edges:
            g[a].append(b)
            g[b].append(a)
        res = [0]*n
        sz = [1]*n
        def dfs(u,fa):
            for v in g[u]:
                if v!=fa:
                    dfs(v,u)
                    sz[u] += sz[v]
                    res[u] += res[v]+sz[v]
        dfs(0,-1)
        def dfs(u,fa):
            for v in g[u]:
                if v!=fa:
                    res[v] = res[u]+n-sz[v]-sz[v]
                    dfs(v,u)
        dfs(0,-1)
        return res

127 ms