0655:输出二叉树(★)
目录
题目
给你一棵二叉树的根节点 root ,请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ,用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则:
- 树的 高度 为
height,矩阵的行数m应该等于height + 1。 - 矩阵的列数
n应该等于2height+1 - 1。 - 根节点 需要放置在 顶行 的 正中间 ,对应位置为
res[0][(n-1)/2]。 - 对于放置在矩阵中的每个节点,设对应位置为
res[r][c],将其左子节点放置在res[r+1][c-2height-r-1],右子节点放置在res[r+1][c+2height-r-1]。 - 继续这一过程,直到树中的所有节点都妥善放置。
- 任意空单元格都应该包含空字符串
""。
返回构造得到的矩阵 res 。
示例 1:
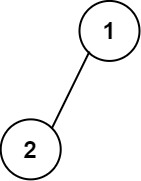
输入:root = [1,2] 输出: [["","1",""], ["2","",""]]
示例 2:
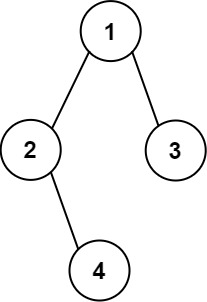
输入:root = [1,2,3,null,4] 输出: [["","","","1","","",""], ["","2","","","","3",""], ["","","4","","","",""]]
提示:
- 树中节点数在范围
[1, 210]内 -99 <= Node.val <= 99- 树的深度在范围
[1, 10]内
分析
观察发现 n = (2«m)-1。于是先递归求得二叉树高度 m,便可以初始化结果数组 res。
然后遍历二叉树,节点在 res 中的行号 x 可以由父节点推得,然而列号 y 不能直接推得。
观察发现节点的子树在 res 中的左右边界 y1、y2 可以由父节点的左右边界推得,而 y = (y1+y2) // 2。 因此遍历时传递 x、y1、y2 即可。
解答
|
|
44 ms