0505：迷宫 II（★）

力扣第 505 题

题目

迷宫中有一个球，它有空地 (表示为 0) 和墙 (表示为 1)。球可以向上、向下、向左或向右滚过空地，但直到撞上墙之前它都不会停止滚动。当球停止时，它才可以选择下一个滚动方向。

给定 m × n 的迷宫(maze)，球的起始位置 (start = [startrow, startcol]) 和目的地 (destination = [destinationrow, destinationcol])，返回球在目的地 (destination) 停止的最短距离。如果球不能在目的地 (destination) 停止，返回 -1。

距离是指球从起始位置 ( 不包括 ) 到终点 ( 包括 ) 所经过的空地数。

你可以假设迷宫的边界都是墙 ( 见例子 )。

示例 1:

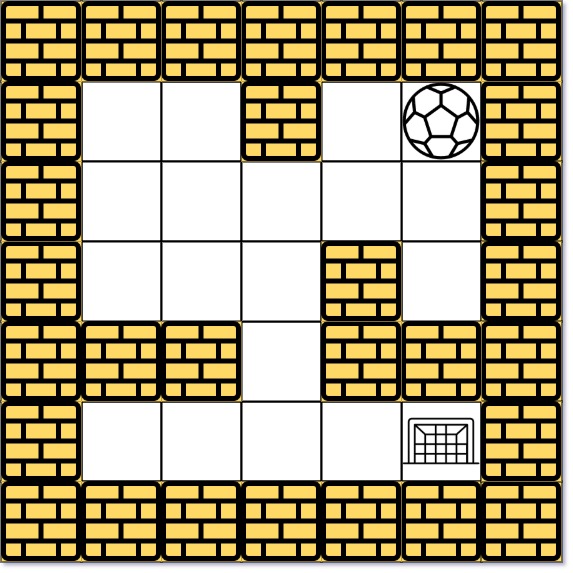
输入: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
输出: 12
解析: 一条最短路径 : left -> down -> left -> down -> right -> down -> right。
总距离为 1 + 1 + 3 + 1 + 2 + 2 + 2 = 12。

示例 2:

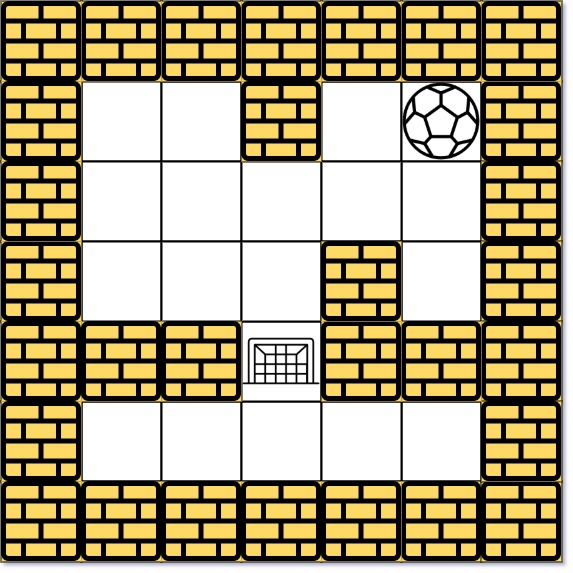
输入: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2]
输出: -1
解析: 球不可能在目的地停下来。注意，你可以经过目的地，但不能在那里停下来。

示例 3:

输入: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1]
输出: -1

注意:

• m == maze.length
• n == maze[i].length
• 1 <= m, n <= 100
• maze[i][j] 是 0 或 1.
• start.length == 2
• destination.length == 2
• 0 <= startrow, destinationrow < m
• 0 <= startcol, destinationcol < n
• 球和目的地都存在于一个空地中，它们最初不会处于相同的位置。

• 迷宫至少包含两个空地。

分析

0490 进阶版，注意距离是看空地个数，因此每次滚动的权重是变化的，要用 dijkstra 而不是 bfs。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

def shortestDistance(self, maze: List[List[int]], start: List[int], destination: List[int]) -> int:
	m, n = len(maze), len(maze[0])
	pq,d = [(0, *start)], {}
	while pq:
		w, i, j = heappop(pq)
		if [i, j] == destination:
			return w
		if (i, j) in d:
			continue
		d[(i, j)] = w
		for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
			x, y, w2 = i, j, w
			while 0<=x+dx<m and 0<=y+dy<n and maze[x+dx][y+dy]==0:
				x, y, w2 = x+dx, y+dy, w2+1
			if (x, y) not in d:
				heappush(pq, (w2, x, y))
	return -1

92 ms