力扣第 407 题
题目
给你一个 m x n 的矩阵,其中的值均为非负整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。
示例 1:

输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后,雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。
示例 2:
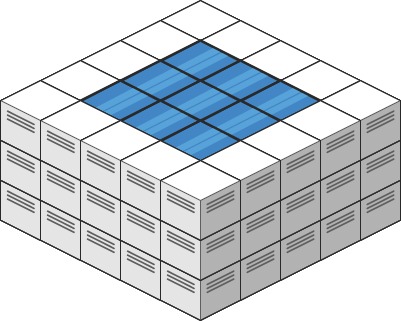
输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10
提示:
m == heightMap.lengthn == heightMap[i].length1 <= m, n <= 2000 <= heightMap[i][j] <= 2 * 104
相似问题:
分析
#1
- 可以将下雨看作动态的过程,假如下到高度 h 时,某个柱子上的雨水能流出去,该柱子能接的最大高度即是 h
- 雨水能否流出去是一个连通性问题,因此可以考虑用并查集
- 从低到高遍历所有柱子,维护连通性,高度 h 时与边界连通的即加到结果中
- 最后再减去柱子本身的高度即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution:
def trapRainWater(self, heightMap: List[List[int]]) -> int:
def find(x):
if f[x]!=x:
f[x]=find(f[x])
return f[x]
def union(x,y):
fx,fy = find(x),find(y)
if fx!=fy:
f[fx]=fy
sz[fy]+=sz[fx]
H = heightMap
m,n = len(H),len(H[0])
f = list(range(m*n+1))
sz = [1]*(m*n+1)
d = defaultdict(list)
for i,j in product(range(m),range(n)):
d[H[i][j]].append((i,j))
res,pre=0,1
for h in sorted(d):
for i,j in d[h]:
if i in [0,m-1] or j in [0,n-1]:
union(i*n+j,m*n)
for x,y in [(i+1,j),(i,j+1),(i-1,j),(i,j-1)]:
if 0<=x<m and 0<=y<n and H[x][y]<=h:
union(i*n+j,x*n+y)
cur = sz[find(m*n)]
res += (cur-pre)*h-len(d[h])*h
pre = cur
return res
|
272 ms
#2
- 还可以借鉴 0042 的双指针思想,从外到内遍历
- 对于最外圈,先找到最低柱子 a
- 则对于 a 相邻的柱子 b,能接到的雨水即是 max(0,a-b)
- 然后将 a 替换为 b,形成新的外圈,并更新 b 的高度为 max(a,b)
- 逐步缩小外圈即可得到每个位置能接到的雨水
- 每轮要找外圈里的最低柱子,用堆维护即可
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def trapRainWater(self, heightMap: List[List[int]]) -> int:
H = heightMap
m,n = len(H),len(H[0])
pq = []
for i, j in product(range(m), range(n)):
if i in [0, m-1] or j in [0, n-1]:
heappush(pq, (H[i][j], i, j))
H[i][j] = -1
res = 0
while pq:
h,i,j = heappop(pq)
for x, y in [(i+1, j), (i-1, j), (i, j-1), (i, j+1)]:
if 0<=x<m and 0<=y<n and H[x][y]!=-1:
res += max(0,h-H[x][y])
heappush(pq, (max(h,H[x][y]),x,y))
H[x][y] = -1
return res
|
168 ms

