0363：矩形区域不超过 K 的最大数值和（★★）

2015-12-29 约 417 字预计阅读 1 分钟次阅读

力扣第 363 题

题目

给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。

题目数据保证总会存在一个数值和不超过 k 的矩形区域。

示例 1：

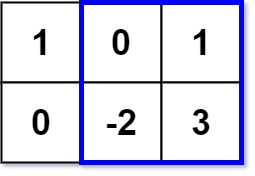
输入：matrix = [[1,0,1],[0,-2,3]], k = 2
输出：2
解释：蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。

示例 2：

输入：matrix = [[2,2,-1]], k = 3
输出：3

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-100 <= matrix[i][j] <= 100
-10⁵ <= k <= 10⁵

进阶：如果行数远大于列数，该如何设计解决方案？

分析

矩形区域的个数是 $O(M^2N^2)$ 级别，光遍历就会超时了。因此要考虑不完全遍历的方法：

左右边界固定为 <j1,j2> 时，求出每一行 [j1,j2] 的区间和，得到数组 A
问题转为求 A 中不超过 k 的最大区间和，可以用前缀和+有序集合解决
预先保存每一行的前缀和，即可快速求出每一行 [j1,j2] 的区间和

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution:
    def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int:
        from sortedcontainers import SortedList
        m,n = len(matrix),len(matrix[0])
        P = [list(accumulate([0]+row)) for row in matrix]
        res = -inf
        for j1 in range(n):
            for j2 in range(j1,n):
                A = [row[j2+1]-row[j1] for row in P]
                A = list(accumulate([0]+A))
                sl = SortedList()
                for a in A:
                    pos = sl.bisect_left(a-k)
                    if pos<len(sl) and a-sl[pos]>res:
                        res = a-sl[pos]
                    sl.add(a)
        return res

2104 ms

目录

0363：矩形区域不超过 K 的最大数值和（★★）

题目

分析

解答