0317：离建筑物最近的距离（★★）

Ian

2015-11-13 约 541 字预计阅读 2 分钟次阅读

力扣第 317 题

题目

给你一个 m × n 的网格，值为 0 、 1 或 2 ，其中:

每一个 0 代表一块你可以自由通过的空地
每一个 1 代表一个你不能通过的建筑
每个 2 标记一个你不能通过的障碍

你想要在一块空地上建造一所房子，在 最短的总旅行距离 内到达所有的建筑。你只能上下左右移动。

返回到该房子的 最短旅行距离 。如果根据上述规则无法建造这样的房子，则返回 -1 。

总旅行距离 是朋友们家到聚会地点的距离之和。

使用 曼哈顿距离 计算距离，其中距离 (p1, p2) = |p2.x - p1.x | + | p2.y - p1.y | 。

示例 1：

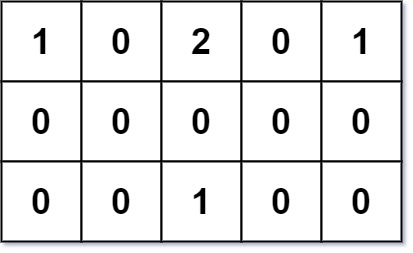
输入：grid = [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]]
输出：7
解析：给定三个建筑物 (0,0)、(0,4) 和 (2,2) 以及一个位于 (0,2) 的障碍物。
由于总距离之和 3+3+1=7 最优，所以位置 (1,2) 是符合要求的最优地点。
故返回7。

示例 2:

输入: grid = [[1,0]]
输出: 1

示例 3:

输入: grid = [[1]]
输出: -1

提示:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 是 0, 1 或 2
grid 中至少有一幢建筑

分析

典型的 bfs。从每个建筑开始遍历，求得空地到每个建筑的距离，总和最小的空地即为所求。

遍历时，注意记录空地能到达的建筑个数，若小于总建筑个数，则不符合要求

可以直接用grid 记录，为了与障碍区分，可以记录为负数

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution:
    def shortestDistance(self, grid: List[List[int]]) -> int:
        def bfs(i,j,k):
            Q, vis = deque([(0,i,j)]), {(i,j)}
            while Q:
                w,i,j = Q.popleft()
                for x,y in [(i+1,j),(i-1,j),(i,j+1),(i,j-1)]:
                    if 0<=x<m and 0<=y<n and grid[x][y]==-k:
                        Q.append((w+1,x,y))
                        grid[x][y]-=1
                        dis[(x,y)] += w+1

        m, n = len(grid), len(grid[0])
        dis, k = defaultdict(int), 0
        for i,j in product(range(m),range(n)):
            if grid[i][j]==1:
                bfs(i,j,k)
                k += 1
        return min([w for (x,y),w in dis.items() if grid[x][y]==-k],default=-1)

2640 ms

目录

0317：离建筑物最近的距离（★★）

题目

分析

解答