0305：岛屿数量 II（★★）

力扣第 305 题

题目

给你一个大小为 m x n 的二进制网格 grid 。网格表示一个地图，其中，0 表示水，1 表示陆地。最初，grid 中的所有单元格都是水单元格（即，所有单元格都是 0）。

可以通过执行 addLand 操作，将某个位置的水转换成陆地。给你一个数组 positions ，其中 positions[i] = [ri, ci] 是要执行第 i 次操作的位置 (ri, ci) 。

返回一个整数数组 answer ，其中 answer[i] 是将单元格 (ri, ci) 转换为陆地后，地图中岛屿的数量。

岛屿 的定义是被「水」包围的「陆地」，通过水平方向或者垂直方向上相邻的陆地连接而成。你可以假设地图网格的四边均被无边无际的「水」所包围。

示例 1：

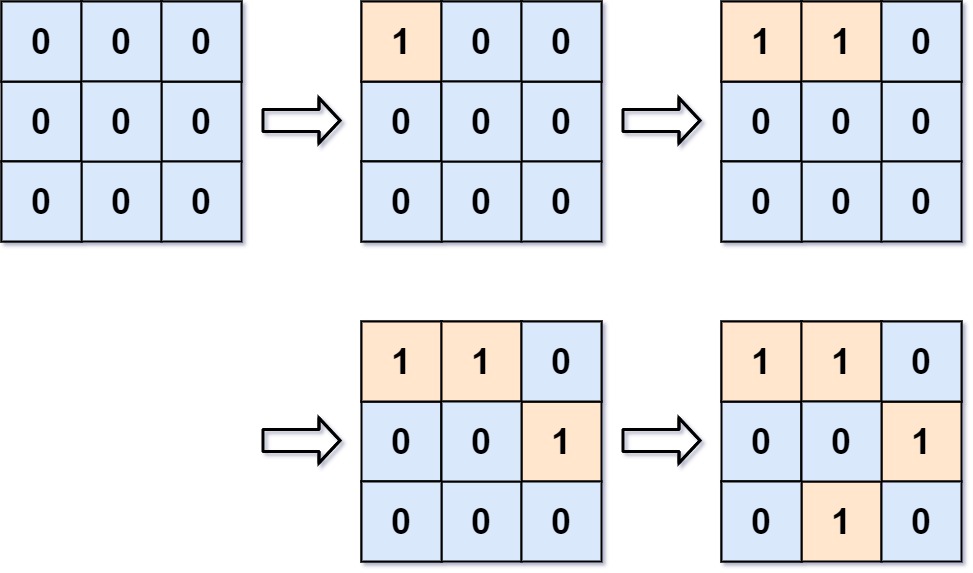
输入：m = 3, n = 3, positions = [[0,0],[0,1],[1,2],[2,1]]
输出：[1,1,2,3]
解释：
起初，二维网格 grid 被全部注入「水」。（0 代表「水」，1 代表「陆地」）
- 操作 #1：addLand(0, 0) 将 grid[0][0] 的水变为陆地。此时存在 1 个岛屿。
- 操作 #2：addLand(0, 1) 将 grid[0][1] 的水变为陆地。此时存在 1 个岛屿。
- 操作 #3：addLand(1, 2) 将 grid[1][2] 的水变为陆地。此时存在 2 个岛屿。
- 操作 #4：addLand(2, 1) 将 grid[2][1] 的水变为陆地。此时存在 3 个岛屿。

示例 2：

输入：m = 1, n = 1, positions = [[0,0]]
输出：[1]

提示：

• 1 <= m, n, positions.length <= 104
• 1 <= m * n <= 104
• positions[i].length == 2
• 0 <= ri < m
• 0 <= ci < n

进阶：你可以设计一个时间复杂度 O(k log(mn)) 的算法解决此问题吗？（其中 k == positions.length）

分析

典型的并查集，维护并查集的块的个数即可。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def numIslands2(self, m: int, n: int, positions: List[List[int]]) -> List[int]:
    def find(x):
        if f.setdefault(x, x) != x:
            f[x] = find(f[x])
        return f[x]

    def union(x, y):
        fx, fy = find(x), find(y)
        if fx != fy:
            f[fx] = fy
            self.cnt -= 1

    res, f, self.cnt = [], {}, 0
    for i, j in positions:
        if (i, j) not in f:
            f[(i, j)] = (i, j)
            self.cnt += 1
            for x, y in [(i-1, j), (i+1, j), (i, j-1), (i, j+1)]:
                if (x, y) in f:
                    union((x, y), (i, j))
        res.append(self.cnt)
    return res

252 ms