0304：二维区域和检索 - 矩阵不可变（★）

力扣第 304 题

题目

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

示例 1：

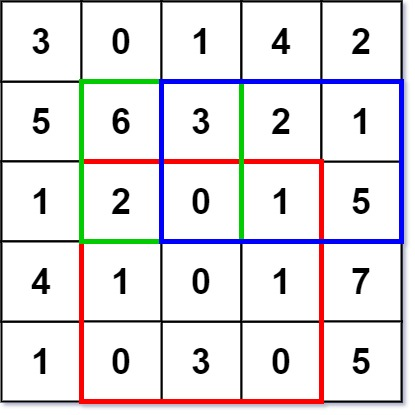
输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -105 <= matrix[i][j] <= 105
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 104 次 sumRegion 方法

相似问题：

• 0303：区域和检索 - 数组不可变
• 0308：二维区域和检索 - 可变
• 3030：找出网格的区域平均强度（1896 分）

分析

• 0303 的升级版，需要用二维前缀和
• 令 $ P[i][j] = \sum_{\substack {0 \le r<i \\ 0 \le c<j }} matrix[r][c] $
• 则 $sumRegion(r1, c1, r2, c2) = P[r2+1][c2+1] -P[r1][c2+1]-P[r2+1][c1]+P[r1][c1]$

解答

1
2
3
4
5
6
7
8
9

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        self.P = [[0]+list(accumulate(col)) for col in zip(*matrix)]
        self.P = [[0]+list(accumulate(col)) for col in zip(*self.P)]


    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return self.P[row2+1][col2+1]-self.P[row1][col2+1]-self.P[row2+1][col1]+self.P[row1][col1]

355 ms