0296：最佳的碰头地点（★★）

力扣第 296 题

题目

给你一个 m x n 的二进制网格 grid ，其中 1 表示某个朋友的家所处的位置。返回 最小的 总行走距离 。

总行走距离 是朋友们家到碰头地点的距离之和。

我们将使用 曼哈顿距离 来计算，其中 distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y| 。

示例 1：

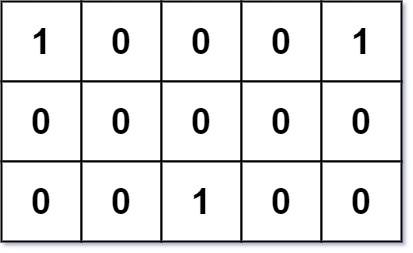
输入: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
输出: 6 
解释: 给定的三个人分别住在(0,0)，(0,4) 和 (2,2):
(0,2) 是一个最佳的碰面点，其总行走距离为 2 + 2 + 2 = 6，最小，因此返回 6。

示例 2:

输入: grid = [[1,1]]
输出: 1

提示:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• grid[i][j] == 0 or 1.
• grid 中 至少 有两个朋友

分析

用 A 保存所有位置的 x 坐标，A 的中位数即是最佳位置的 x 坐标。y 坐标同理。

解答

1
2
3
4
5
6

def minTotalDistance(self, grid: List[List[int]]) -> int:
    def cal(grid):
        A = [i for i, row in enumerate(grid) for val in row if val==1]
        half = len(A) // 2
        return sum(A[-half:])-sum(A[:half])
    return cal(grid)+cal(zip(*grid))

40 ms