0133：克隆图（★）

力扣第 133 题

题目

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
public int val;
public List<Node> neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

示例 1：

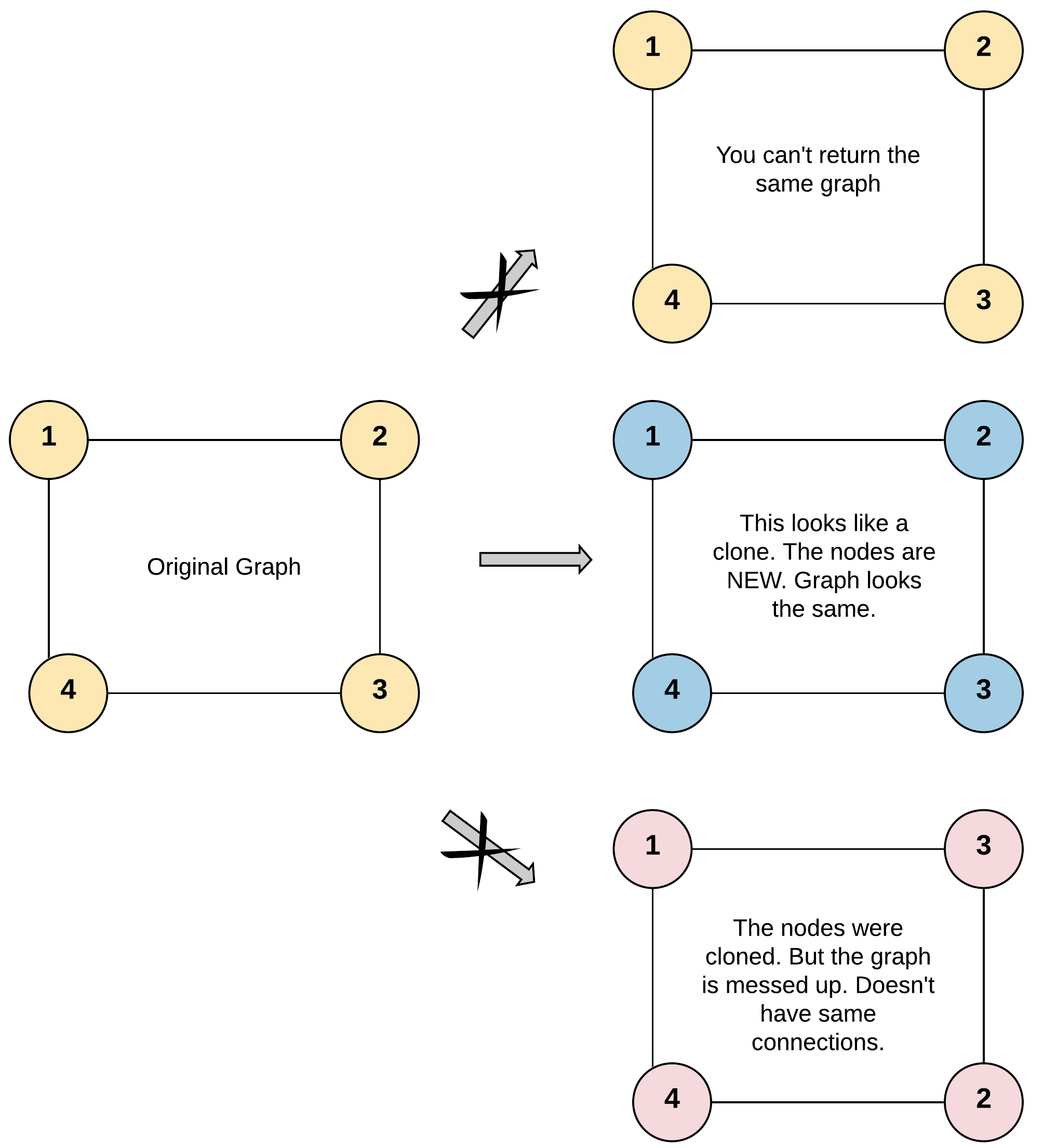
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

提示：

• 这张图中的节点数在 [0, 100] 之间。
• 1 <= Node.val <= 100
• 每个节点值 Node.val 都是唯一的，
• 图中没有重复的边，也没有自环。
• 图是连通图，你可以从给定节点访问到所有节点。

分析

#1

• 遍历时维护 <原节点,克隆节点> 的映射 d，即可解决循环的问题
• 遍历到节点 u ，若 u 在 d 中则跳过
• 若 u 不在 d 中，只克隆值得到节点 u’，保存映射 <u,u’> 到 d
• 继续遍历 u 的邻居列表，并将遍历后的克隆添加到 u’ 的邻居列表即可

用 dfs 遍历，注意不能用 d.get(v, dfs(v)) 来简化。即使元素在 dict 中，dict.get 的 default 也会执行，只不过不返回该值。

1
2
3
4
5
6
7
8

class Solution:
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        def dfs(u):
            d[u] = Node(u.val)
            d[u].neighbors = [d[v] if v in d else dfs(v) for v in u.neighbors]
            return d[u]
        d = {}
        return dfs(node) if node else None

43 ms

#2

也可以用 bfs 遍历，注意入队前就应克隆，防止重复入队。

解答

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution:
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        if not node:
            return None
        d = {node:Node(node.val)}
        sk = [node]
        while sk:
            u = sk.pop()
            for v in u.neighbors:
                if v not in d:
                    d[v] = Node(v.val)
                    sk.append(v)
                d[u].neighbors.append(d[v])
        return d[node]

42 ms